Dish or Parabola: Difference between revisions
(added gain formula) |
|||
| Line 34: | Line 34: | ||
the gain of a dish antenna (compared to an isotropic standard) can be calculated thus: | the gain of a dish antenna (compared to an isotropic standard) can be calculated thus: | ||
<math> Gdbi = 10\times \mbox{log} \left( \eta \frac {4 \pi}{\lambda^2}A \right) </math> | <math> Gdbi = 10\times \mbox{log} \left( \eta \frac {4 \pi}{\lambda^2}A \right) </math> where: | ||
<math> \eta </math> is the efficiency of the dish | |||
<math> A </math> is the area of the dish | |||
<math> \lambda </math> is the wavelength of the signal | |||
For practical purposes, the most critical measurement affecting the gain (regardless of dish size) of a dish antenna has been found to be placing the feedpoint exactly at the focal length '''f'''. Paul Wade - [http://www.qsl.net/n1bwt/preface.htm W1GHZ], gives the following relative gain measurements for a 22inch dish with <math> \frac{f}{D} =0.39 </math> operating at 10GHz: | |||
{| style="width:55" border = "1" | {| style="width:55" border = "1" | ||
Revision as of 14:16, 6 August 2008
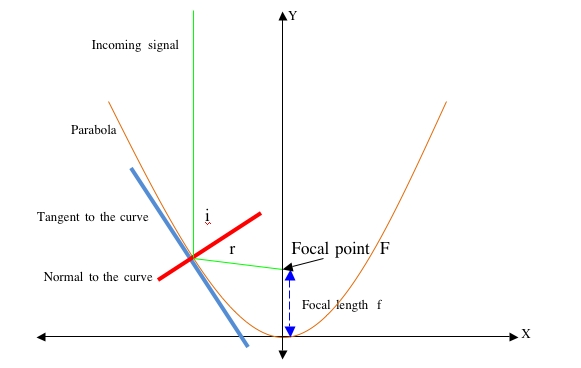
Parabolic Geometry
A Parabola is one of the “conic sections” and is defined as the locus (path) of a point that travels so that it is equidistant from a fixed point and a straight line. Algebraically this can be reduced to:
<math> y = ax^2</math> where a is a constant
More specifically, <math> y = \frac{x^2}{4f} </math> where f is the focal length – distance from the curve to the focal point
In the diagram above:
- the Y axis is central to the curve
- the tangent is a line that touches the curve at one point and has the same gradient as the curve at that point
- the normal is perpendicular to the tangent at the point of contact with the curve
- i is the angle of incidence – the angle between the incoming signal and the normal
- r is the angle of reflection – the angle between the reflected signal and the normal
- i = r Angle of incidence = Angle of reflection
- a broad beam entering the parabola will be reflected to and concentrated at the focal point
During receive, the signal is concentrated at the focal point F. During transmit, a feed point at F will produce a beam of RF energy.
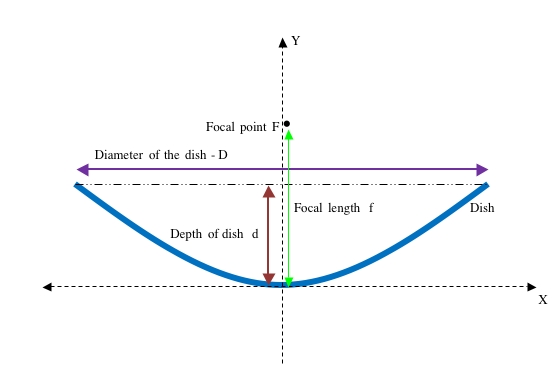
Finding the focal length of a parabolic dish
<math> f = \frac {D^2}{16d} </math> where D is the diameter of the dish and d is the depth of the dish
Gain of a dish antenna
Related wiki page - Gain
the gain of a dish antenna (compared to an isotropic standard) can be calculated thus:
<math> Gdbi = 10\times \mbox{log} \left( \eta \frac {4 \pi}{\lambda^2}A \right) </math> where:
<math> \eta </math> is the efficiency of the dish
<math> A </math> is the area of the dish
<math> \lambda </math> is the wavelength of the signal
For practical purposes, the most critical measurement affecting the gain (regardless of dish size) of a dish antenna has been found to be placing the feedpoint exactly at the focal length f. Paul Wade - W1GHZ, gives the following relative gain measurements for a 22inch dish with <math> \frac{f}{D} =0.39 </math> operating at 10GHz:
| Feed distance | Relative gain |
| 8.125" | -0.6dB |
| 8.250" | 0dB |
| 8.375" | -0.3dB |
| 8.625" | -1.7dB |