Dish or Parabola

Parabolic Geometry

A Parabola is one of the “conic sections” and is defined as the locus (path) of a point that travels so that it is equidistant from a fixed point and a straight line. Algebraically this can be reduced to:

<math> y = ax^2</math> where a is a constant

More specifically, <math> y = \frac{x^2}{4f} </math> where f is the focal length – distance from the curve to the focal point

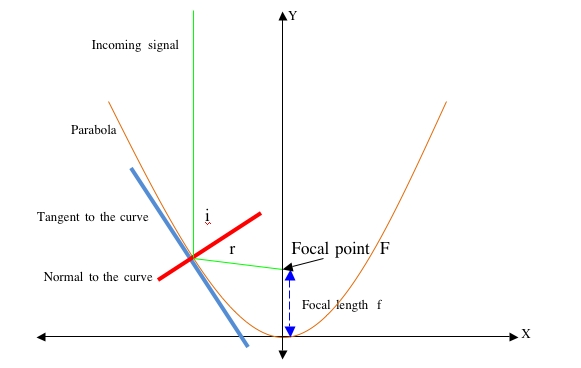
In the diagram above:

• the Y axis is central to the curve
• the tangent is a line that touches the curve at one point and has the same gradient as the curve at that point
• the normal is perpendicular to the tangent at the point of contact with the curve
• i is the angle of incidence – the angle between the incoming signal and the normal
• r is the angle of reflection – the angle between the reflected signal and the normal
• i = r Angle of incidence = Angle of reflection
• a broad beam entering the parabola will be reflected to and concentrated at the focal point

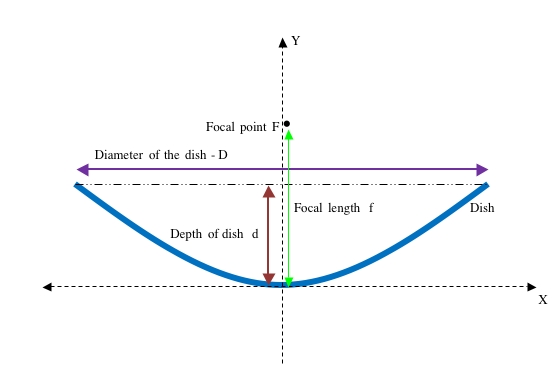
Finding the focal length of a parabolic dish

<math> f = \frac {D^2}{16d} </math> where D is the diameter of the dish and d is the depth of the dish